算法:二叉树创建及前序遍历

题目描述

给定一个二叉树，返回它的前序遍历

1.创建二叉链表的节点类

public class TreeNode {
    
    public var val: String
    // leftChild就指向左节点的内存地址
    public var leftChild: TreeNode?
    // 而rightChild就指向右节点的内存地址
    public var rightChild: TreeNode?
    
    public init(_ val: String) {
        self.val = val
        self.leftChild = nil
        self.rightChild = nil
    }
}

2.前序创建二叉树类

class GeneralBinaryTree {
    // 根节点
    var rootNode: TreeNode!
    fileprivate var items: Array<String>
    fileprivate var index = -1
    
    init(items: Array<String>) {
        self.items = items
        self.rootNote = createTree()
    }
    // 以先序递归的方式创建二叉树
    fileprivate func createTree() -> TreeNode?{
        // 索引加一
        self.index = self.index + 1
        if index < self.items.count && index >= 0 {
            
            let item = self.items[index]
            
            if item == "" {
                return nil
            } else {
               
                let node =  TreeNode.init(item)
                node.leftChild = createTree()  // 递归创建左子树
                node.rightChild = createTree() // 递归创建右子树
                return node
            }
        }
        return nil
    }
}

理解递归创建左子树/右子树,如图

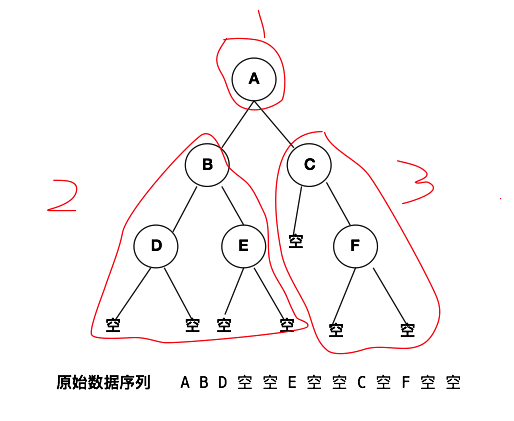
binaryTree

从上面的分析我们不难看出，我们要先创建根节点，然后创建左子树，最后创建右子树。因为左子树和右子树都是二叉树，所以创建左子树和右子树是原问题的子问题。也就是说子问题与原问题解决方案一致，这种情况下就可以使用递归的思想来解决

这样外界通过一个数组就可以生成一个二叉树对象

将items数组中存储的值转换成二叉链表的存储结构。items数组中的空字符串，表明该节点为空

let items: Array<String> = ["A", "B", "D", "", "", "E", "", "", "C", "","F", "", ""]
let generalBinaryTree: GeneralBinaryTree = GeneralBinaryTree(items: items)

3.二叉树的前序遍历

extension GeneralBinaryTree {
 
    // 前序遍历：先遍历根节点，再遍历左子树，让后遍历右子树
    public func preOrderTraversal() {
        print("先序遍历递归版本：")
        self.preOrderTraversal(node: rootNode)
        // A B D 空 空 E 空 空 C 空 F 空 空
        print("\n")
        
//        print("先序遍历while版本：")
//        let array = self.preOrderTraversal2(node: rootNode)
//        print(array) // ["A", "B", "D", "E", "C", "F"]
    }
    
    // 递归版本
    private func preOrderTraversal(node: TreeNode?) {
        // 节点为nil,打印"空"
        guard let node = node else {
            print("空", separator: "", terminator: " ")
            return
        }
        print(node.val, separator: "", terminator: " ")
        
        // 递归遍历左子树
        preOrderTraversal(node: node.leftChild)
        
        // 递归遍历右子树
        preOrderTraversal(node: node.rightChild)
    }
    
    // while循环版本
    private func preOrderTraversal2(node: TreeNode?)->[String] {

        if node == nil {
            return []
        }
        var cur = node
        var treeStack = [TreeNode]()
        // 排序数组
        var res = [String]()
        while cur != nil || treeStack.isEmpty == false {
            if cur != nil{
                treeStack.append(cur!)
                res.append(cur!.val)
                cur = cur?.leftChild
            }else{
                cur = treeStack.removeLast().rightChild
            }
        }
        return res
    }
}